A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation
본 포스팅은 논문 A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation를 읽고 정리한 내용입니다.
아는 것이 많이 없어서 부족한 부분이 많습니다. 혹여나 틀린부분 있다면 지적해주시길 바랍니다!
ICRA 2007
Anastasios I. Mourikis and Stergios I. Roumeliotis
Abstract
EKF를 기반으로 real-time vision inertial navigation 고안
EKF의 state vector에서 3D feature position이 포함된 measurement model이 필요로 하지 않음
Introduction
Inertial sensor는 저렴하고 small-scale의 Pose estimation (mobile robot, UAV)에 적합.
GPS는 신뢰도가 낮은 편(실내, urban canyon 등) 카메라는 낮은 비용, 낮은 무게, 낮은 전력 소모
카메라는 많은 양의 환경정보를 갖고 있음 → 이것이 Pose를 추정하는데 어려움이 있음
Real-time localization에서 Computational Complexity와 estimation accuracy는 trade-off 관계
Visual feature를 Multiple measurement로하여 localization함
여러 카메라포즈에서 본 static한 feature를 geometric constraints로 이용
Related work
생략
III. ESTIMATOR DESCRIPTION
A. Structure of the EKF state vector
IMU state vector
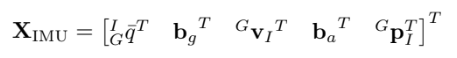
${ }_{G}^{I} \bar{q}^{T}$는 frame {G}에서 frame { I }로의 Unit quaternion 이다.
${ }^{G} \mathbf{p}{I}, { }^{G} \mathbf{v}{I}$는 각각 IMU의 global postion과 velocity 이다.
IMU bias는 random walk process이며 white Gaussian noise vector $\mathbf{n}{wg}$와 $\textbf{n}{wa}$로부터 이끌어 낼 수 있다.
IMU error-state vector
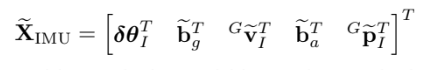
보통 error는 값에서 추정값을 뺀 $\widetilde{x}=x-\hat{x}$ 형태 이지만 error quaternion은 조금 다르게 정의 한다.
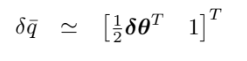
여기서 1은 스칼라이기 때문에 error equaternion의 자유도는 3 자유도가 된다.
N개의 카메라 포즈가 포함된 EKF state vector는
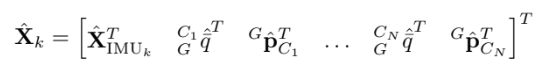
error state는
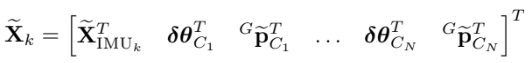
B. Propagation
filter propagation 식은 연속 시간에서의 시스템 모델에서 이산화를 거쳐 유도된다.
우선 연속 시간 시스템을 모델링한다.
1) Continuous-time system modeling
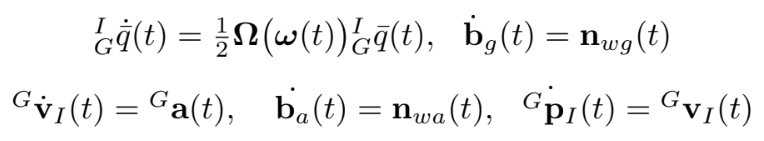
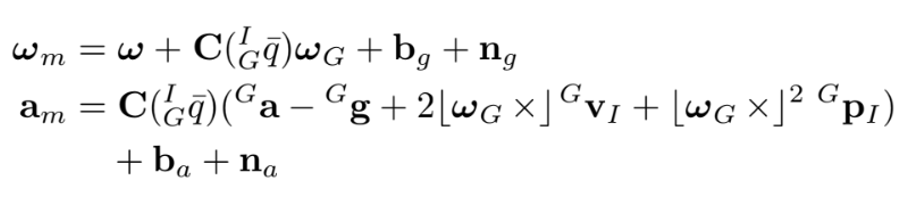
$\mathbf{C}(\cdot)$는 rotation matrix, $\mathbf{n}{g}, \mathbf{n}{a}$는 zero-mean white Gaussian noise이다.
IMU measurement는 행성의 자전의 정보 $\omega_G$를 포함하고, 중력 가속도 ${}^Gg$도 존재한다.
IMU state의 ‘추정’에 관한 식은
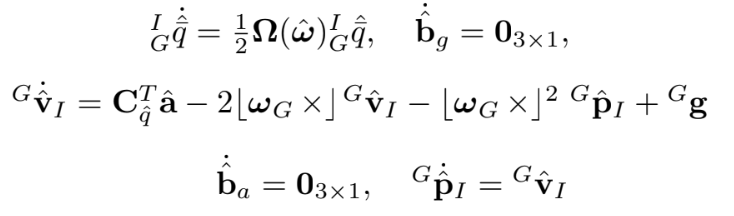
$\mathbf{C}{\hat{q}}=\mathbf{C}\left({ }{G}^{I} \hat{\bar{q}}\right)$
$\hat{\mathbf{a}}=\mathbf{a}{m}-\hat{\mathbf{b}}{a}$
$\hat{\boldsymbol{\omega}}=\boldsymbol{\omega}{m}-\hat{\mathbf{b}}{g}-\mathbf{C}{\hat{q}} \boldsymbol{\omega}{G}$
IMU state의 Linearized continuous-time model은
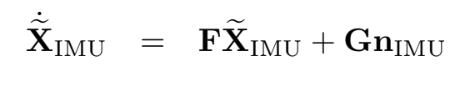
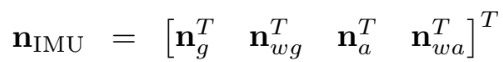
위에서 살펴본 IMU error state는
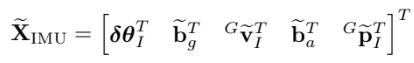
이다.
$\textbf{F}$와 $\textbf{G}$는
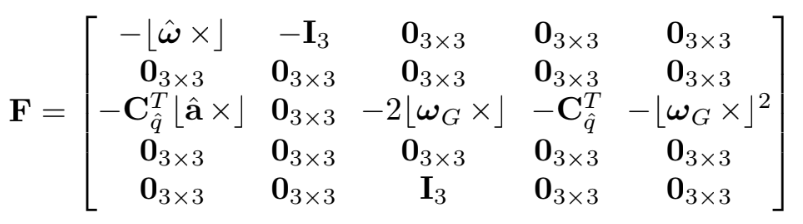
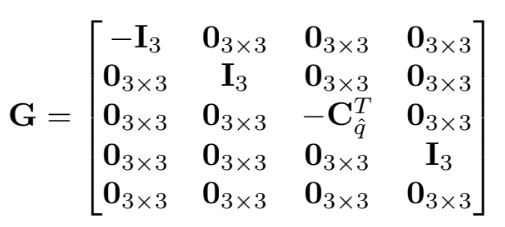
2) Discrete-time implementation
IMU state 추정은 5th order Runge-Kutta 방법으로 propagate하고, EKF를 위해서는 covariance도 propagate 해야 한다.
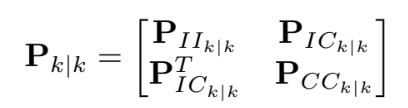
$\mathbf{P}{I I{k \mid k}}$는 IMU state의 covariance이고 15 x 15 이다. (IMU state가 15 x 1 이기 때문에)
$\mathbf{P}{C C{k \mid k}}$는 camera pose 추정의 covariance matrix이고 6N x 6N 이다.
( 카메라 포즈 하나 당 6개 - rotation+translation, 그리고 이것들이 N개 )
$\mathbf{P}{I C{k \mid k}}$는 IMU state error와 camera pose 추정 간의 correlation
위의 covariance는 다음과 같이 propagate 된다
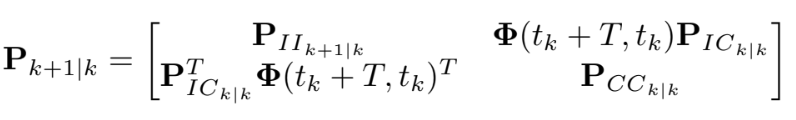
$\mathbf{P}{I I{k+1 \mid k}}$은 Lyapunov equation의 수치 적분으로 구할 수 있다.
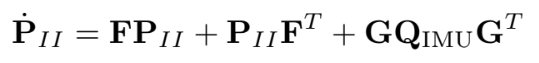
state transition은 미분방정식의 수치 적분으로 구할 수 있다.
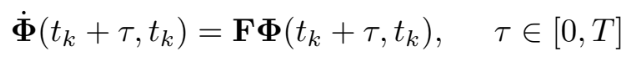
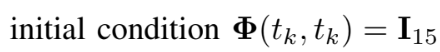
C. State Augmentation
새로운 이미지가 들어오면 IMU pose 추정으로부터 camera pose 추정을 구한다.
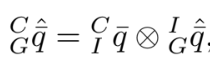

${ }{I}^{C} \bar{q}$와 ${ }^{I} \mathbf{p}{C}$는 known
새로운 이미지의 camera pose를 얻어냈으므로 새로운 Covariance가 필요하다.
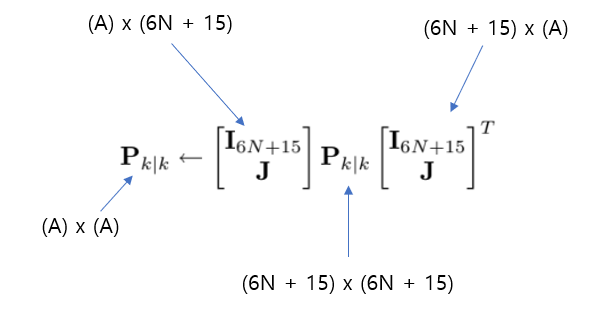
D. Measurement Model
EKF를 사용하기 위해 residual을 다음과 같이 정의
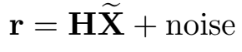
여기서 noise는 zero-mean, white이며 state error와 uncorrelated 되어야 한다.
매 순간의 카메라 포즈 대신에 측정된 feature를 camera observation으로하고 측정 된 같은 3D 점은 constraint로 작용한다.
feature가 1개($f_j$) 있다고 가정할 때 $M_j$는 camera pose들로부터 observed 된 것이라 하자
그 관찰된 1개 feature에 대한 model은

j = feature 번호
i = j 번호의 feature를 공통으로 관찰한 카메라들 중 하나
Camera frame에서의 feature position은

unknown한 feature position(관찰한 feature의 global 좌표)을 예측하여 에러를 최소화 시킨다.
measurement residual는 다음과 같다
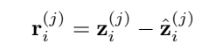
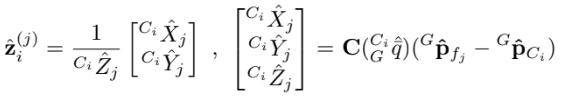
residual을 linearize하면
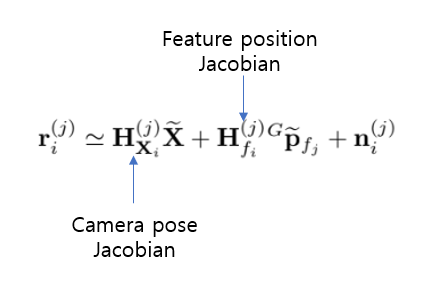
$\mathbf{H}{\mathbf{X}{i}}^{(j)} ,\mathbf{H}{f{i}}^{(j)}$는 measurement Jacobian임
그래서 $M_j$안에 속하는 모든 measurement의 residual들을 쌓아다가 다음의 식으로 만든다
(밑의 식을 보면 i가 없어진 걸 알 수 있음)
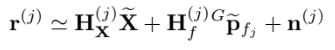
j feature를 관찰할 모든 measurement의 residual을 쌓은 것이다.
근데 state 추정 $\textbf{X}$는 feature position 추정하는데 ${ }^{G} \widetilde{\mathbf{p}}{f{j}}$ 는 $\tilde{\textbf{X}}$ 와 correlated함 따라서
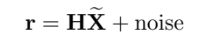
꼴이 아니므로 EKF의 emasurement update를 못한다.
그래서 행렬 $\mathbf{H}^{(j)}_{f}$의 left nullspace에 $\mathbf{r}^{(j)}$를 projection 시켜서 새롭게 정의하고, 특히나 $\mathbf{A}$의 column이 $\mathbf{H}_f$의 left nullspace의 basis를 갖는 unitary 행렬이라 했을 때 다음과 같다.
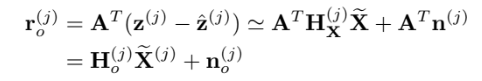
$2M_j\times3$인 $\mathbf{H}^{(j)}{f}$행렬이 full column rank면 nullspace의 차원은 $2M_j-3$이다.
그러므로 $\mathbf{r}^{(j)}{o}$는 $(2M_j-3)\times1$ 벡터이다.
또한 이 residual은 feature coordinate 상에서 독립이므로 EKF 업데이트가 가능하다.
A가 unitary이므로 covariance matrix는
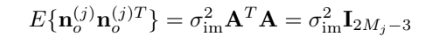
epipolar 같은 경우 $M_j*(M_j-1)/2$로 계산량이 많은 반면 이 방법으로 $2M_j-3$ 개의 독립된 constraint로 대응 될 수 있으므로 계산적인 면에서 매우 효과적이다.
E. EKF updates
둘 중 하나의 조건일 때 업데이트 된다.
- 몇 개의 이미지가 더 이상 detect 되지 않을 때
- 새로운 이미지가 들어올 때마다 현재 카메라 포즈가 state vector에 포함된다. 만약 최대 허용 가능한 카메라 포즈의 수($N_{max}$)에 도달하면, 오래된 것들 중 하나 이상 제거한다. 삭제되기전에 모든 feature observation 정보를 사용 .(논문 참고)
제거 하기 전에 모든 feature observation를 localization information으로 사용 N_max/3의 균일한 시간 간격을 갖는 포즈를 선택, EKF 업데이트 후 삭제
L개의 feaeture를 발견했다면 residual vector를 계산
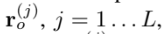
그리고 그에 맞는 measurement 행렬을 구한다.
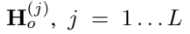
전부 쌓아서 하나의 residual vector로 만든다.
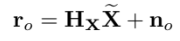
feature measurement들은 독립이고 noise vector는 uncorrelated함
그러므로 covariance matrix는
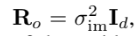
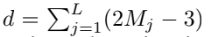
d가 좀 큰 수가 될 수 있는데 예를 들어 10개의 feature와 10개의 camera pose면 residual vector의 차원은 170개인데 이걸 EKF update에 그대로 쓰면 시간 오래걸린다.
그래서 $\textbf{H}_{\textbf{X}}$를 QR decomposition으로 해서 구함
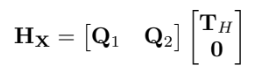
$\textbf{Q}1,\textbf{Q}_2$는 column이 range와 $\textbf{H}{\textbf{X}}$의 nullspace base가 되고 $\textbf{T}_{\textbf{H}}$는 upper triangular matrix이다.
그럼 다음과 같은 식이 가능하다.
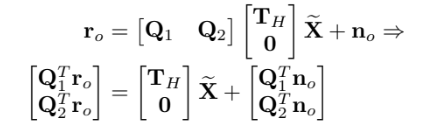
마지막줄이 noise에만 관련된 식이므로 버리기 가능하다.
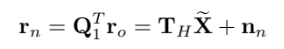
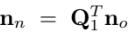
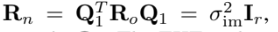
EKF update는 kalman gain으로 업데이트한다.
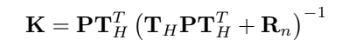
correction은 vector에서 주어진다.
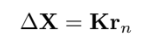
state covariance matrix 업데이트는
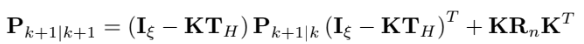
ξ = 6N+15 차원
EKF 컴퓨팅 최대 차원은
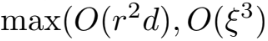
만약 residual vector $\textbf{r}0$이 주어졌는데 $\textbf{H}{\textbf{X}}$로 project 안하면 $O(d^3)$이고 $d \gg \xi, r$이므로 업데이트가 비효율 적이다.
'SLAM' 카테고리의 다른 글
| Visual-Inertial Odometry of Aerial Robots (5) | 2022.08.30 |
|---|---|
| A micro Lie theory for state estimation in robotics (4) (6) | 2022.08.25 |
| A micro Lie theory for state estimation in robotics (3) (2) | 2022.08.25 |
| A micro Lie theory for state estimation in robotics (2) (7) | 2022.08.21 |
| A micro Lie theory for state estimation in robotics (1) (2) | 2022.08.18 |
