본 포스팅은 논문 A micro Lie theory for state estimation in robotics를 읽고 정리한 내용입니다.
아는 것이 많이 없어서 부족한 부분이 많습니다. 혹여나 틀린부분 있다면 지적해주시길 바랍니다!
DIFFERENTIATION RULES ON MANIFOLDS
앞에서 manifold에서의 derivation에 대해 정의했으니 성질에 대해서 알아보자
A. The chain rule
Manifold에서의 Jacobian chain rule
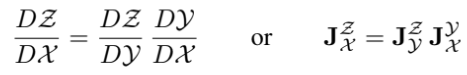
미적분학에 나온 chain rule과 비슷함
간단한 증명방법은 오른쪽 Jacobian 일 때 작은 $\boldsymbol{\tau}$에 대해 다음이 성립한다고 했었다.
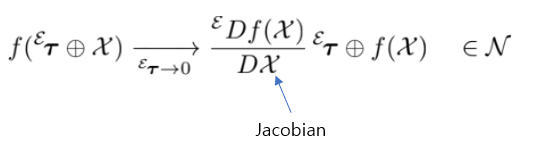
그대로 적용해보면
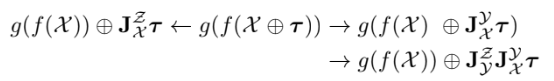
right,left cross Jacobian에 대해서도 성립한다
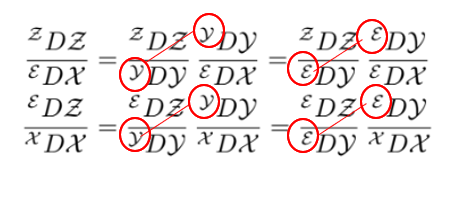
간단하게 증명하자면
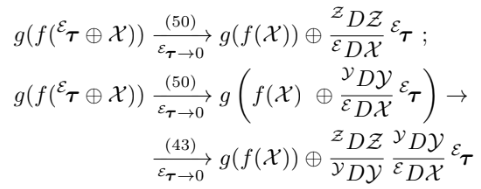
미적분학에서 배운 chain rule이랑 매우 유사한 형태임을 알 수 있다.
B. Elemetary Jacobian blocks
Jacobian의 몇가지 성질에 대해서 배운다
가볍게 보고 지나가자
1 ) Inverse
정의
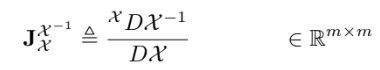
이용할 성질들
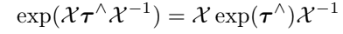
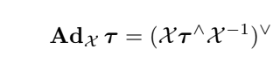
결과는
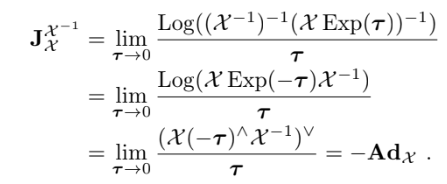
2 ) Composition
정의
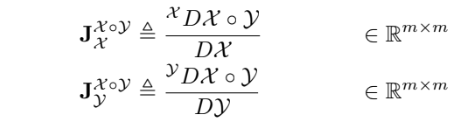
이용할 성질들
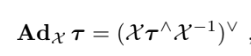
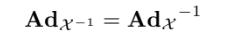
결과는
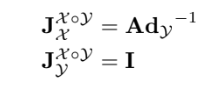
3 ) Jacobians of $\mathcal{M}$
manifold의 right Jacobian을 정의
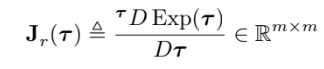
$\mathbf{J}$ 아랫첨자로 r이 있는데 right라는 뜻임, 그리고 매우작은 $\delta\boldsymbol{\tau}$에 대해 다음이 성립
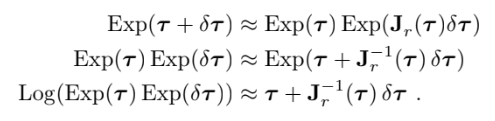
right 했으니 left도 하자
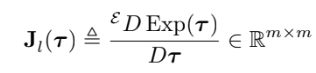
이번엔 $\mathbf{J}$ 아랫첨자로 l이 있는데 left라는 뜻임, 그리고 매우작은 $\delta\boldsymbol{\tau}$에 대해 다음이 성립
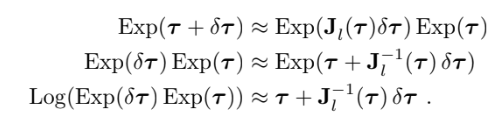
그리고 right의 성질과
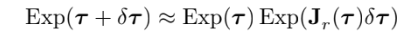
left의 성질로
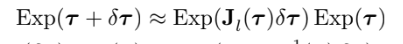
adjoint를 이끌어 낼 수 있다
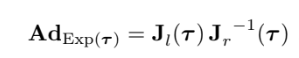
또한 chain rule로 left와 right의 관계도 이끌어 낼 수 있음!
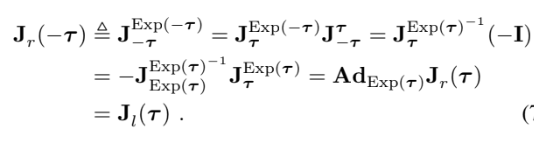
4 ) Group action
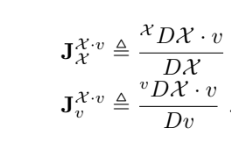
C. Useful, but deduced, Jacobian blocks
1 ) Log map
$\tau=\log (\mathcal{X})$에 대해
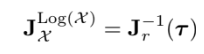
2 ) Plus and minus
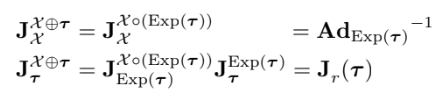
그리고 $\mathcal{Z}=\mathcal{X}^{-1} \circ \mathcal{Y}$ 와 $\boldsymbol{\tau}=\mathcal{Y} \ominus \mathcal{X}=\log (\mathcal{Z})$가 주어졌을 때
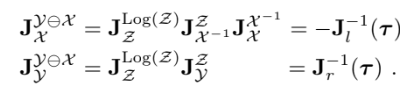
첫번째 줄 증명
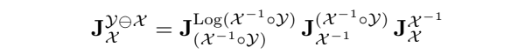
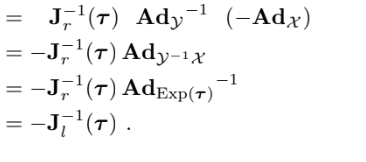
'SLAM' 카테고리의 다른 글
| A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation (1) | 2022.08.30 |
|---|---|
| Visual-Inertial Odometry of Aerial Robots (1) | 2022.08.30 |
| A micro Lie theory for state estimation in robotics (3) (0) | 2022.08.25 |
| A micro Lie theory for state estimation in robotics (2) (0) | 2022.08.21 |
| A micro Lie theory for state estimation in robotics (1) (0) | 2022.08.18 |
