본 포스팅은 논문 A micro Lie theory for state estimation in robotics를 읽고 정리한 내용입니다.
아는 것이 많이 없어서 부족한 부분이 많습니다. 혹여나 틀린부분 있다면 지적해주시길 바랍니다!
G. Derivatives on Lie groups
Lie group에서 쓰이는 derivative를 유도하는 파트임
Jacobian은 domain이 변경되는 연산임을 기억하자
1 ) Reminder: Jacobians on vector spaces
다변수 함수의 Jacobian은 $f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}$ 일 때 다음과 같다
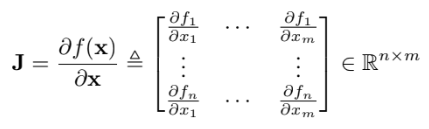
벡터의 형태로 다르게 표현 해보면
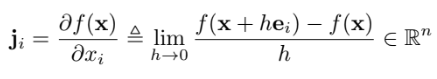

$\mathbf{J}=\left[\mathbf{j}{1} \cdots \mathbf{j}{m}\right]$, $\mathbf{j}{i}=\left[\frac{\partial f{1}}{\partial x_{i}} \cdots \frac{\partial f_{n}}{\partial x_{i}}\right]^{\top}$
$\textbf{e}_i$는 $\mathbb{R}^{m}$의 i번째 basis
2 ) Right Jacobians on Lie groups
다변수 함수의 Jacobian은 $f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}$ domain이 변경되는 반면 manifold에서는 $f: \mathcal{M} \rightarrow \mathcal{N}$ 로 domain이 변경 된다.
앞의 플러스 연산, 마이너스 연산으로 manifold에서의 일반적인 derivation을 보자.
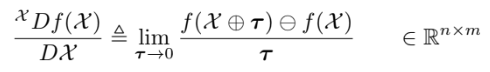
이를 right Jacobian이라 말한다.
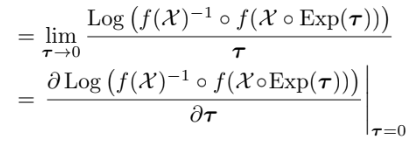
그리고 다변수 함수와 모양이 비슷하다
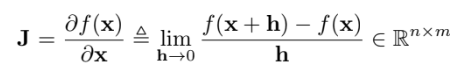
right Jacobian은 local tangent space를 mapping한다
작은 $\boldsymbol{\tau}$에 대해 다음이 성립
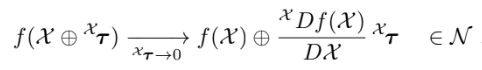
3 ) Left Jacobians on Lie groups
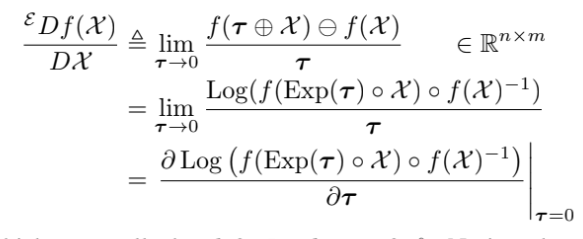
left jacobian은 global tangent space를 mapping한다.
작은 $\boldsymbol{\tau}$에 대해 다음이 성립
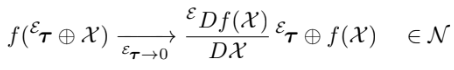
4 ) Crossed right–left Jacobians
간단하게 말해서 출발지와 목적지가 정해지면 직접적으로 갈 수도 있지만 우회해서 다른 길로도 갈 수 있다고 생각하면 될 것 같다.
우선 식을 보자

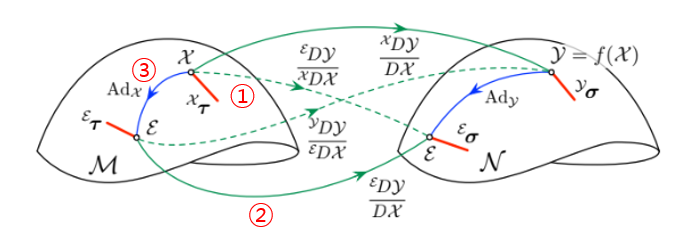
아까 보았던식 일부를 보면
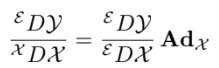
위의 그림에서 ① 경로는 ② 경로와 ③ 경로를 합친 것임을 알 수 있다.
H. Uncertainty in manifolds, covariance propagation
local perturbations $\boldsymbol{\tau}$를 점 $\overline{\mathcal{X}} \in \mathcal{M}$에서의 tangent space $T_{\overline{\mathcal{X}}} \mathcal{M}$위에서 다음과 같이 정의 할 수 있다.
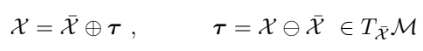
여기서 $\boldsymbol{\tau}$는 manifold 위의 $\overline{\mathcal{X}}$의 tangent space 위의 uncertainty라고 하자
Covariance matrix는 보통 정의하는 것처럼 Expectation을 이용해 정의한다
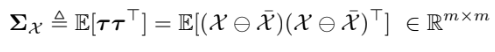
이제 manifold 위에서의 Gaussian 분포를 말할 수 있다.
$\mathcal{X} \sim \mathcal{N}\left(\overline{\mathcal{X}}, \boldsymbol{\Sigma}_{\mathcal{X}}\right)$
local을 알아봤으니 global을 uncertainty를 알아보자
global은 왼쪽 연산이므로
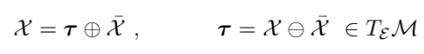
local과 global covarinace 간의 관계는
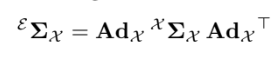
Covariance propagation의 linearization은

I. Discrete integration on manifolds
Exponential map은 연속 시간에 대한 함수로 되어 있는데 이걸 이산적인(discrete) 함수로 바꾸고 싶다 (컴퓨터로 계산 하려면)
아이디어는 이동경로를 조각내서 합하는 것이다.
어느 점에서 어느 점까지 tangent space 상에서 이동(속도 x 시간)한 뒤 exponential map을 취해 manifold 점으로 끌어온다.
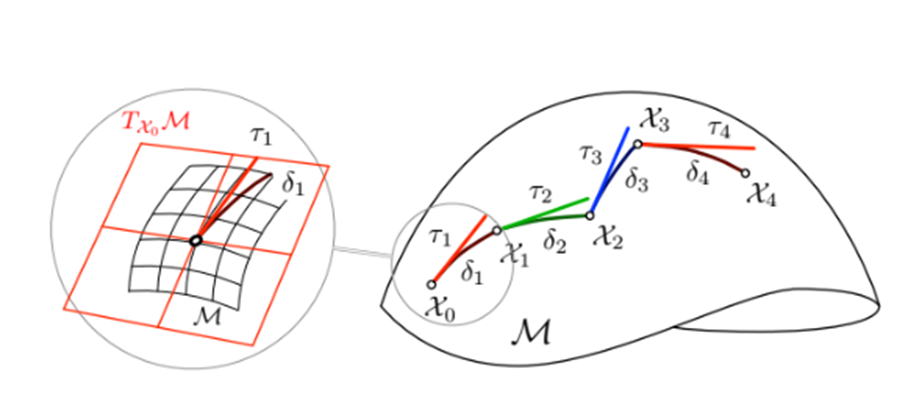

이렇게 recursive한 형태로도 씀

'SLAM' 카테고리의 다른 글
| A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation (3) | 2022.08.30 |
|---|---|
| Visual-Inertial Odometry of Aerial Robots (5) | 2022.08.30 |
| A micro Lie theory for state estimation in robotics (4) (6) | 2022.08.25 |
| A micro Lie theory for state estimation in robotics (2) (7) | 2022.08.21 |
| A micro Lie theory for state estimation in robotics (1) (2) | 2022.08.18 |
