본 포스팅은 논문 A micro Lie theory for state estimation in robotics를 읽고 정리한 내용입니다.
아는 것이 많이 없어서 부족한 부분이 많습니다. 혹여나 틀린부분 있다면 지적해주시길 바랍니다!
Abstract
로봇 state estimation에 Lie theory를 써야할 때가 있는데
Lie theory의 전체를 공부하는 것보다는 필요한 부분만 효율적으로 작성함
Introduction
생략
A micro Lie Thoery
A. The Lie group
Lie group이란 smooth manifold 위의 특정 group을 말한다.
※smooth manifold 설명: https://ko.wikipedia.org/wiki/매끄러운_다양체
Group은 집합 $\mathcal{G}$와 연산 $\circ$ 이 집합 원소 $\mathcal{X}, \mathcal{Y}, \mathcal{Z} \in \mathcal{G}$에 대해 다음 4가지 조건을 만족 시킨다.
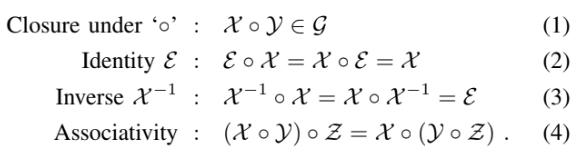
표기는 이런 식으로 함 $(\mathcal{G}, \circ)$
B. The group actions
Lie group은 회전, 이동, 등과 같이 다른 집합으로 transform을 하는 경우가 있는데
action이란 이러한 집합에서 다른 집합으로 변형하는 것을 말한다.
Lie group $\mathcal{X}$ 와 집합 $\mathcal{V}$가 주어졌을 때 action의 표기는 $\mathcal{X} \cdot v$ 으로 한다. $(\mathcal{X} \in \mathcal{M} \text \ ,\ v \in \mathcal{V})$

위의 식은 $\cdot$ 연산에 대한 정의이다.
$①$: Lie group $\mathcal{X}$ 와 집합 $\mathcal{V}$의 결과는 집합 $\mathcal{V}$에 속하게 된다.
$②$: $\mathcal{X} \in \mathcal{M}$ 과 $v \in \mathcal{V}$의 $\cdot$ 연산에 대한 표기는 다음과 같이 한다.
몇 가지 예를 들어보면
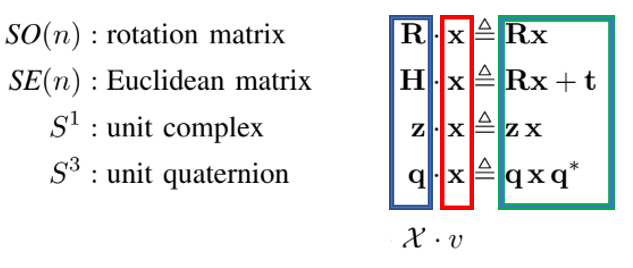
$SO(n)$은 회전 행렬만 모아 놓은 군, $SE(n)$은 회전과 이동을 모아 놓은 군, $S^1$은 2D 복소공간, $S^3$은 쿼터니언 공간이다.
파란색 네모 박스에 속한 것들은 각각의 smooth manifold에 속하는 원소들이며 이들의 집합은 smooth manifold를 이루고 있다.
그리고 빨간색 박스는 특정 집합을 말하며 여기 서는 좌표(위치)를 의미한다.
초록색 박스는 action에 대한 정의이다.
어떤 좌표에 대한 집합( $v$ )이 회전 공간($\mathcal{X}$)에서 회전을 해도( $\cdot$ ) 결과가 좌표( $v$ )가 나온다는 것은
$①$을 만족시킴을 알 수 있다.
C. The tangent spaces and the Lie algebra
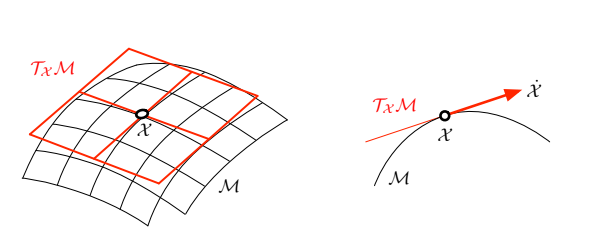
Lie group의 manifold $\mathcal{M}$ 위에서 시간에 따라 움직이는 점 $\mathcal{X}(t)$가 있을 때
특정 위치 $\mathcal{X}$에서의 속도는 $\dot{\mathcal{X}}=\partial \mathcal{X} / \partial t$이며, 이는 $\mathcal{M}$위의 점 $\mathcal{X}$의 tangent space에 속해 있다 .
(그림 참고)
$\mathcal{M}$ 위의 점 $\mathcal{X}$의 tangent space의 표기는 다음과 같이 한다 $T_{\mathcal{X}} \mathcal{M}$
$\mathcal{M}$은 smooth manifold이므로 한 점, 한 점마다 각각의 tangent space 존재한다.
1 ) The Lie algebra $\mathfrak{m}$
특정 위치 $\mathcal{X}$에서가 아닌 identity $\mathcal{E}$에서의 tangent space를 $\mathcal{M}$위의 Lie algebra라고 한다.

Lie algebra는 다음과 같은 사실을 이끌어 낸다.
- Lie algebra $\mathfrak{m}$은 vector space이다. 그리하여 $\mathbb{R}^{m}$상에 있는 벡터들로 확정 지을 수 있고, $m$차원은 $\mathcal{M}$의 자유도 (Degrees of freedom)와 같다.
- exponential map $\exp : \mathfrak{m} \rightarrow \mathcal{M}$은 정확히 Lie algebra의 원소를 group의 원소로 변환한다.
log map은 이의 역연산이다.
- $\mathcal{X}$위의 tangent space안의 벡터들은 linear transform을 통해서 identity $\mathcal{E}$위의 tangent space로 변경할 수 있다. 이 변형을 adjoint라고 한다. (수많은 tangent space가 있으므로 identity를 기준으로 잡는 느낌)
Lie algebra는 ‘hat’ 기홀 표시한다.
속도의 Lie algebra는 $\mathbf{v}^{\wedge}$, 혹은 일반적으로는 $\boldsymbol{\tau}^{\wedge}=(\mathbf{v} t)^{\wedge}=\mathbf{v}^{\wedge} t$ 로 표기한다.
왼쪽 윗첨자에 특정한 tangent space를 표기하기도한다.
$^\mathcal{X}{\mathbf{v}} ^\wedge \in T_{\mathcal{X}} \mathcal{M} \text { , } ^\mathcal{E}{\mathbf{v}}^{\wedge} \in T_{\mathcal{E}} \mathcal{M}$ (이렇게)
multiplicative group은 $\mathcal{X}^{-1} \dot{\mathcal{X}}+\mathcal{X}^{-1} \mathcal{X}=0$ 이라는 constraint를 갖는다.
바로 group의 성질 때문이다.
$\text { Inverse } \mathcal{X}^{-1}: \mathcal{X}^{-1} \circ \mathcal{X}=\mathcal{X} \circ \mathcal{X}^{-1}=\mathcal{E}$
※multiplicative group 이기 때문에 $\circ$ 연산이 곱연산이다.
요 성질에서 미분을 하면 앞서 말한 constraint를 얻을 수 있다.
얻은 constraint로 Lie algebra를 다음과 같이 정의한다.
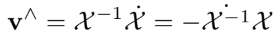
2 ) The Cartesian vector space $\mathbb{R}^{m}$
Lie algebra의 원소 $\tau^{\wedge}$는 generator라 불리는 $E_i$를 이용해 linear combination으로 표현이 가능하다.
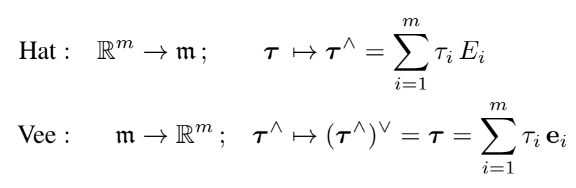
$\boldsymbol{\tau}$는 $\mathbb{R}^m$상의 벡터이다. ($\mathbf{e}_{i}^{\wedge}=E_{i})$
$SO(3)$ group의 Lie algebra $\mathfrak{s o}(3)$ 예제

'SLAM' 카테고리의 다른 글
| A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation (3) | 2022.08.30 |
|---|---|
| Visual-Inertial Odometry of Aerial Robots (5) | 2022.08.30 |
| A micro Lie theory for state estimation in robotics (4) (6) | 2022.08.25 |
| A micro Lie theory for state estimation in robotics (3) (2) | 2022.08.25 |
| A micro Lie theory for state estimation in robotics (2) (7) | 2022.08.21 |
